
Picturing Mental Math
By Wendy Petti
Help students become more mathematically literate by giving them the tools for quick mental math.
When we use math in the "real world," we often need to come up with a quick number mentally in a few moments: How many more minutes until the end of class? How much will three tickets cost? What's my score now? We can help students become more mathematically literate by giving them tools and strategies for quick mental math.
The way we calculate mentally is not the way we calculate with paper and pencil. Students often are resistant to that notion; they try to use an invisible paper and a finger in the air or an imaginary pencil when "forced" to do mental math. It's easy to understand why they do that; it's what theyre accustomed to. It's not so easy to lead them into a new way of calculating, in which we take away not only their paper and pencil, but also their paper-and-pencil methods.
We can help students develop a mental math tool bag by modeling the tools concretely. Think of this transitional stage as mental math with training wheels. Now, let's take a look at some tools for picturing math linearly.
NUMBER LINE
To help students develop a "mental number line," or a linear mental picture when adding or subtracting numbers, it can be effective to post a large number line (from 0 -100) at the front of the classroom and to use it regularly. Highlight all the multiples of 10; they serve as "anchors." Point to the number line with a yardstick to model how to jump along a number line to add or subtract two-digit numbers or skip-count by a given number.
When students are learning to skip-count as a strategy for learning multiplication tables, it helps to show them how they can "bridge" a ten: break a number into two chunks to jump to the nearest 10 and then jump beyond. For instance, skip-counting by 7s might look like this when students are starting out:
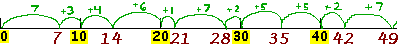 |
The yardstick follows this pattern of jumps, touching on each anchor, as well as on each multiple of 7. At first, a teacher or student can "narrate" the jumps: "Jump 7; jump 3 and then 4 to 14; jump 6 and then 1 to 21; jump 7 to 28; jump 2 and then 5 to 35." After a few repetitions of narrated jumps, the yardstick jumping with bridging can be done silently as the class recites the 7s aloud. Eventually, the jumping can be done without bridging:
 |
The same approach can be applied to skip-counting by higher numbers, bridging tens as needed.
It can be helpful for each student to have a personal number line as well. You can use meter sticks with the tens highlighted for that purpose. However, we want to guide students away from counting by ones, as many students do in the lower grades. It helps to model jumping in chunks, as students use a finger to jump along a personal number line. Another strategy is to lay Cuisenaire rods along the meter stick.
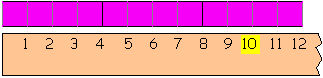 |
Â
PARTIALLY NUMBERED LINE
Do we really need all the numbers labeled when using the number line as a tool, or do they get in the way? After considerable number line activity with the tens highlighted as anchors, switch to number lines with only the tens marked:
 |
With sufficient preparatory number line work, students should find it comfortable to skip-count, add, and subtract on a partially numbered line, using a finger or pencil to jump by tens and bridge the anchoring tens as needed. For example, to add 38 + 35, the student could start at 38 (by placing a pencil or finger to the left of 40), jump by 10 three times: 48, 58, 68 (placing the pencil to the left of 50, 60, and 70); jump 2 to reach 70; and then jump 3 more (ending about 1/3 of the distance between 70 and 80). The sparsely-numbered line makes it easier to think in terms of chunks.
EMPTY NUMBER LINE
An "empty number line" is, just as the name suggests, a line without numbers. Students can add and subtract multi-digit numbers using an empty number line to record their steps, drawing jumps and writing a few numbers as needed.
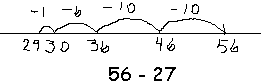 |
With the "jump strategy" used on empty number lines, students treat one number as a whole number and break the other number into manageable chunks. In order to use an empty number line or mental number line effectively, students need to be able to count by 10s, on and off the decade, and to jump across -- or bridge -- tens. Let's look at how those two skills are applied in the samples. In the addition example, the student begins with 56 near the left end of the line, jumps two tens, and then breaks the 7 into 4 + 3 to be able to jump to the 80 and then jump the remaining amount. In the subtraction example, the student begins with 56 near the right end of the line, jumps back two tens, jumps back 6 to reach 30, and then jumps back 1 more. For subtracting a number such as 39, a student probably would find it most efficient to jump back 40 and then jump forward 1; this is a "compensation strategy."
Those examples demonstrate that it is not necessary for a number line or an empty number line to begin at 0. It is helpful for students to be able to focus on the portion of the number line they actually need for solving a problem.
As students become more adept using empty number lines, they can solve problems with fewer steps; instead of jumping by ten at a time, they might be able to jump all the tens in one jump (jump 30, or 40, or more, as called for in the problem). They might not need to record as much information. Eventually, they might be able to leave off the numbers altogether. At that point, theyre probably well-equipped for using their mental number line.
Empty number lines have become common teaching tools in the Netherlands and Australia. In "The Empty Number Line: A Useful Tool or Just Another Procedure?," Australian Janette Bobis describes her daughter's eventual enthusiasm for the empty number line after initial resistance. She finds it "easier to use [than paper and pencil algorithms] because
- she understands how it works (it represents her thinking);
- it keeps a record of each step in her thinking;
- it allows her to track errors; and
- it enables her to think about what to do next when the computation is too demanding to do solely in her head.?
VISUALIZING ELAPSED TIME
Some students do well when visualizing a clock face with the hands moving around and around, but a linear model works well, too. Students can use a partially-numbered timeline or an empty timeline for this work.
 |
For example, to calculate the elapsed time between 9:45 a.m. and 2:10 p.m., jumps might look like this:
 |
With the timeline approach, it is easy to see that the elapsed time is 4 hours, 25 minutes.
USING MENTAL TOOLS
There are many more tools we can place in a mental math tool bag. We want to give students a large tool bag, not just one tool. This article focuses on number line tools, because a mental number line is quite likely the most flexible, adaptable, and powerful tool. Sometimes, however, another mental strategy might prove easier. For example, when adding or subtracting two numbers with no regrouping involved, such as 345 + 612, its probably easier to add the hundreds (300 + 600), then the tens (40 + 10), and then the ones (5 + 2), than it is to jump along a huge mental number line. But the mental number line works well too: Start at 345, jump 600 to 945, jump 10 to 955, jump 2 to 957. Some strategies can be applied with or without visualization. To subtract 98 from 400, we can subtract 100 then add 2; on a mental number line, we can jump back 100 then jump forward 2. We also could add 2, and then subtract 100: 402 - 100. Either way, visualizing helps us understand how to adjust.
For younger students, perhaps the greatest challenge when doing mental math is holding several numbers in the mind at once. Breaking a number into chunks means understanding which chunks will be meaningful, mentally jumping with those chunks, and keeping track of the jumps to arrive at the correct answer. That ability comes with practice. In the meantime, doing mental math with visual training wheels helps build numerical flexibility and agility.
As students become more agile, they can take on larger mental computations, adding and subtracting numbers in the hundreds and even thousands, or skip-counting by any two-digit multiple. It's stimulating and empowering!
Janette Bobis, "The Empty Number Line: A Useful Tool or Just Another Procedure?" Teaching Children Mathematics, NCTM, April 2007, pp. 410-413



 You've reached the end of another grading period, and what could be more daunting than the task of composing insightful, original, and unique comments about every child in your class? The following positive statements will help you tailor your comments to specific children and highlight their strengths.
You can also use our statements to indicate a need for improvement. Turn the words around a bit, and you will transform each into a goal for a child to work toward. Sam cooperates consistently with others becomes Sam needs to cooperate more consistently with others, and Sally uses vivid language in writing may instead read With practice, Sally will learn to use vivid language in her writing. Make Jan seeks new challenges into a request for parental support by changing it to read Please encourage Jan to seek new challenges.
Whether you are tweaking statements from this page or creating original ones, check out our Report Card Thesaurus [see bottom of the page] that contains a list of appropriate adjectives and adverbs. There you will find the right words to keep your comments fresh and accurate.
We have organized our 125 report card comments by category. Read the entire list or click one of the category links below to jump to that list.
AttitudeBehaviorCharacterCommunication SkillsGroup WorkInterests and TalentsParticipationSocial SkillsTime ManagementWork Habits
Attitude
The student:
is an enthusiastic learner who seems to enjoy school.
exhibits a positive outlook and attitude in the classroom.
appears well rested and ready for each day's activities.
shows enthusiasm for classroom activities.
shows initiative and looks for new ways to get involved.
uses instincts to deal with matters independently and in a positive way.
strives to reach their full potential.
is committed to doing their best.
seeks new challenges.
takes responsibility for their learning.
Behavior
The student:
cooperates consistently with the teacher and other students.
transitions easily between classroom activities without distraction.
is courteous and shows good manners in the classroom.
follows classroom rules.
conducts themselves with maturity.
responds appropriately when corrected.
remains focused on the activity at hand.
resists the urge to be distracted by other students.
is kind and helpful to everyone in the classroom.
sets an example of excellence in behavior and cooperation.
Character
The student:
shows respect for teachers and peers.
treats school property and the belongings of others with care and respect.
is honest and trustworthy in dealings with others.
displays good citizenship by assisting other students.
joins in school community projects.
is concerned about the feelings of peers.
faithfully performs classroom tasks.
can be depended on to do what they are asked to do.
seeks responsibilities and follows through.
is thoughtful in interactions with others.
is kind, respectful and helpful when interacting with his/her peers
is respectful of other students in our classroom and the school community
demonstrates responsibility daily by caring for the materials in our classroom carefully and thoughtfully
takes his/her classroom jobs seriously and demonstrates responsibility when completing them
is always honest and can be counted on to recount information when asked
is considerate when interacting with his/her teachers
demonstrates his/her manners on a daily basis and is always respectful
has incredible self-discipline and always gets his/her work done in a timely manner
can be counted on to be one of the first students to begin working on the task that is given
perseveres when faced with difficulty by asking questions and trying his/her best
does not give up when facing a task that is difficult and always does his/her best
is such a caring boy/girl and demonstrates concern for his/her peers
demonstrates his/her caring nature when helping his/her peers when they need the assistance
is a model citizen in our classroom
is demonstrates his/her citizenship in our classroom by helping to keep it clean and taking care of the materials in it
can always be counted on to cooperate with his/her peers
is able to cooperate and work well with any of the other students in the class
is exceptionally organized and takes care of his/her things
is always enthusiastic when completing his/her work
is agreeable and polite when working with others
is thoughtful and kind in his/her interactions with others
is creative when problem solving
is very hardworking and always completes all of his/her work
is patient and kind when working with his/her peers who need extra assistance
trustworthy and can always be counted on to step in and help where needed
Communication Skills
The student:
has a well-developed vocabulary.
chooses words with care.
expresses ideas clearly, both verbally and through writing.
has a vibrant imagination and excels in creative writing.
has found their voice through poetry writing.
uses vivid language in writing.
writes clearly and with purpose.
writes with depth and insight.
can make a logical and persuasive argument.
listens to the comments and ideas of others without interrupting.
Group Work
The student:
offers constructive suggestions to peers to enhance their work.
accepts the recommendations of peers and acts on them when appropriate.
is sensitive to the thoughts and opinions of others in the group.
takes on various roles in the work group as needed or assigned.
welcomes leadership roles in groups.
shows fairness in distributing group tasks.
plans and carries out group activities carefully.
works democratically with peers.
encourages other members of the group.
helps to keep the work group focused and on task.
Interests and Talents
The student:
has a well-developed sense of humor.
holds many varied interests.
has a keen interest that has been shared with the class.
displays and talks about personal items from home when they relate to topics of study.
provides background knowledge about topics of particular interest to them.
has an impressive understanding and depth of knowledge about their interests.
seeks additional information independently about classroom topics that pique interest.
reads extensively for enjoyment.
frequently discusses concepts about which they have read.
is a gifted performer.
is a talented artist.
has a flair for dramatic reading and acting.
enjoys sharing their musical talent with the class.
Participation
The student:
listens attentively to the responses of others.
follows directions.
takes an active role in discussions.
enhances group discussion through insightful comments.
shares personal experiences and opinions with peers.
responds to what has been read or discussed in class and as homework.
asks for clarification when needed.
regularly volunteers to assist in classroom activities.
remains an active learner throughout the school day.
Social Skills
The student:
makes friends quickly in the classroom.
is well-liked by classmates.
handles disagreements with peers appropriately.
treats other students with fairness and understanding.
is a valued member of the class.
has compassion for peers and others.
seems comfortable in new situations.
enjoys conversation with friends during free periods.
chooses to spend free time with friends.
Time Management
The student:
tackles classroom assignments, tasks, and group work in an organized manner.
uses class time wisely.
arrives on time for school (and/or class) every day.
is well-prepared for class each day.
works at an appropriate pace, neither too quickly or slowly.
completes assignments in the time allotted.
paces work on long-term assignments.
sets achievable goals with respect to time.
completes make-up work in a timely fashion.
Work Habits
The student:
is a conscientious, hard-working student.
works independently.
is a self-motivated student.
consistently completes homework assignments.
puts forth their best effort into homework assignments.
exceeds expectations with the quality of their work.
readily grasps new concepts and ideas.
generates neat and careful work.
checks work thoroughly before submitting it.
stays on task with little supervision.
displays self-discipline.
avoids careless errors through attention to detail.
uses free minutes of class time constructively.
creates impressive home projects.
Related: Needs Improvement Report Card Comments for even more comments!
Student Certificates!
Recognize positive attitudes and achievements with personalized student award certificates!
Report Card Thesaurus
Looking for some great adverbs and adjectives to bring to life the comments that you put on report cards? Go beyond the stale and repetitive With this list, your notes will always be creative and unique.
Adjectives
attentive, capable, careful, cheerful, confident, cooperative, courteous, creative, dynamic, eager, energetic, generous, hard-working, helpful, honest, imaginative, independent, industrious, motivated, organized, outgoing, pleasant, polite, resourceful, sincere, unique
Adverbs
always, commonly, consistently, daily, frequently, monthly, never, occasionally, often, rarely, regularly, typically, usually, weekly
Copyright© 2022 Education World
You've reached the end of another grading period, and what could be more daunting than the task of composing insightful, original, and unique comments about every child in your class? The following positive statements will help you tailor your comments to specific children and highlight their strengths.
You can also use our statements to indicate a need for improvement. Turn the words around a bit, and you will transform each into a goal for a child to work toward. Sam cooperates consistently with others becomes Sam needs to cooperate more consistently with others, and Sally uses vivid language in writing may instead read With practice, Sally will learn to use vivid language in her writing. Make Jan seeks new challenges into a request for parental support by changing it to read Please encourage Jan to seek new challenges.
Whether you are tweaking statements from this page or creating original ones, check out our Report Card Thesaurus [see bottom of the page] that contains a list of appropriate adjectives and adverbs. There you will find the right words to keep your comments fresh and accurate.
We have organized our 125 report card comments by category. Read the entire list or click one of the category links below to jump to that list.
AttitudeBehaviorCharacterCommunication SkillsGroup WorkInterests and TalentsParticipationSocial SkillsTime ManagementWork Habits
Attitude
The student:
is an enthusiastic learner who seems to enjoy school.
exhibits a positive outlook and attitude in the classroom.
appears well rested and ready for each day's activities.
shows enthusiasm for classroom activities.
shows initiative and looks for new ways to get involved.
uses instincts to deal with matters independently and in a positive way.
strives to reach their full potential.
is committed to doing their best.
seeks new challenges.
takes responsibility for their learning.
Behavior
The student:
cooperates consistently with the teacher and other students.
transitions easily between classroom activities without distraction.
is courteous and shows good manners in the classroom.
follows classroom rules.
conducts themselves with maturity.
responds appropriately when corrected.
remains focused on the activity at hand.
resists the urge to be distracted by other students.
is kind and helpful to everyone in the classroom.
sets an example of excellence in behavior and cooperation.
Character
The student:
shows respect for teachers and peers.
treats school property and the belongings of others with care and respect.
is honest and trustworthy in dealings with others.
displays good citizenship by assisting other students.
joins in school community projects.
is concerned about the feelings of peers.
faithfully performs classroom tasks.
can be depended on to do what they are asked to do.
seeks responsibilities and follows through.
is thoughtful in interactions with others.
is kind, respectful and helpful when interacting with his/her peers
is respectful of other students in our classroom and the school community
demonstrates responsibility daily by caring for the materials in our classroom carefully and thoughtfully
takes his/her classroom jobs seriously and demonstrates responsibility when completing them
is always honest and can be counted on to recount information when asked
is considerate when interacting with his/her teachers
demonstrates his/her manners on a daily basis and is always respectful
has incredible self-discipline and always gets his/her work done in a timely manner
can be counted on to be one of the first students to begin working on the task that is given
perseveres when faced with difficulty by asking questions and trying his/her best
does not give up when facing a task that is difficult and always does his/her best
is such a caring boy/girl and demonstrates concern for his/her peers
demonstrates his/her caring nature when helping his/her peers when they need the assistance
is a model citizen in our classroom
is demonstrates his/her citizenship in our classroom by helping to keep it clean and taking care of the materials in it
can always be counted on to cooperate with his/her peers
is able to cooperate and work well with any of the other students in the class
is exceptionally organized and takes care of his/her things
is always enthusiastic when completing his/her work
is agreeable and polite when working with others
is thoughtful and kind in his/her interactions with others
is creative when problem solving
is very hardworking and always completes all of his/her work
is patient and kind when working with his/her peers who need extra assistance
trustworthy and can always be counted on to step in and help where needed
Communication Skills
The student:
has a well-developed vocabulary.
chooses words with care.
expresses ideas clearly, both verbally and through writing.
has a vibrant imagination and excels in creative writing.
has found their voice through poetry writing.
uses vivid language in writing.
writes clearly and with purpose.
writes with depth and insight.
can make a logical and persuasive argument.
listens to the comments and ideas of others without interrupting.
Group Work
The student:
offers constructive suggestions to peers to enhance their work.
accepts the recommendations of peers and acts on them when appropriate.
is sensitive to the thoughts and opinions of others in the group.
takes on various roles in the work group as needed or assigned.
welcomes leadership roles in groups.
shows fairness in distributing group tasks.
plans and carries out group activities carefully.
works democratically with peers.
encourages other members of the group.
helps to keep the work group focused and on task.
Interests and Talents
The student:
has a well-developed sense of humor.
holds many varied interests.
has a keen interest that has been shared with the class.
displays and talks about personal items from home when they relate to topics of study.
provides background knowledge about topics of particular interest to them.
has an impressive understanding and depth of knowledge about their interests.
seeks additional information independently about classroom topics that pique interest.
reads extensively for enjoyment.
frequently discusses concepts about which they have read.
is a gifted performer.
is a talented artist.
has a flair for dramatic reading and acting.
enjoys sharing their musical talent with the class.
Participation
The student:
listens attentively to the responses of others.
follows directions.
takes an active role in discussions.
enhances group discussion through insightful comments.
shares personal experiences and opinions with peers.
responds to what has been read or discussed in class and as homework.
asks for clarification when needed.
regularly volunteers to assist in classroom activities.
remains an active learner throughout the school day.
Social Skills
The student:
makes friends quickly in the classroom.
is well-liked by classmates.
handles disagreements with peers appropriately.
treats other students with fairness and understanding.
is a valued member of the class.
has compassion for peers and others.
seems comfortable in new situations.
enjoys conversation with friends during free periods.
chooses to spend free time with friends.
Time Management
The student:
tackles classroom assignments, tasks, and group work in an organized manner.
uses class time wisely.
arrives on time for school (and/or class) every day.
is well-prepared for class each day.
works at an appropriate pace, neither too quickly or slowly.
completes assignments in the time allotted.
paces work on long-term assignments.
sets achievable goals with respect to time.
completes make-up work in a timely fashion.
Work Habits
The student:
is a conscientious, hard-working student.
works independently.
is a self-motivated student.
consistently completes homework assignments.
puts forth their best effort into homework assignments.
exceeds expectations with the quality of their work.
readily grasps new concepts and ideas.
generates neat and careful work.
checks work thoroughly before submitting it.
stays on task with little supervision.
displays self-discipline.
avoids careless errors through attention to detail.
uses free minutes of class time constructively.
creates impressive home projects.
Related: Needs Improvement Report Card Comments for even more comments!
Student Certificates!
Recognize positive attitudes and achievements with personalized student award certificates!
Report Card Thesaurus
Looking for some great adverbs and adjectives to bring to life the comments that you put on report cards? Go beyond the stale and repetitive With this list, your notes will always be creative and unique.
Adjectives
attentive, capable, careful, cheerful, confident, cooperative, courteous, creative, dynamic, eager, energetic, generous, hard-working, helpful, honest, imaginative, independent, industrious, motivated, organized, outgoing, pleasant, polite, resourceful, sincere, unique
Adverbs
always, commonly, consistently, daily, frequently, monthly, never, occasionally, often, rarely, regularly, typically, usually, weekly
Copyright© 2022 Education World Back to Geography Lesson Plan
Where Did Foods Originate?
(Foods of the New World and Old World)
Subjects
Arts & Humanities
--Language Arts
Educational Technology
Science
--Agriculture
Social Studies
--Economics
--Geography
--History
----U.S. History
----World History
--Regions/Cultures
Grade
K-2
3-5
6-8
9-12
Advanced
Brief Description
Students explore how New World explorers helped change the Old World's diet (and vice versa).
Objectives
Students will
learn about changes that occurred in the New World and Old World as a result of early exploration.
use library and Internet sources to research food origins. (Older students only.)
create a bulletin-board map illustrating the many foods that were shared as a result of exploration.
Keywords
Columbus, explorers, origin, food, timeline, plants, map, New World, Old World, colonies, colonial, crops, media literacy, products, consumer
Materials Needed:
library and/or Internet access (older students only)
outline map of the world (You might print the map on a transparency; then use an overhead projector to project and trace a large outline map of the world onto white paper on a bulletin board.)
magazines (optional)
Lesson Plan
The early explorers to the Americas were exposed to many things they had never seen before. Besides strange people and animals, they were exposed to many foods that were unknown in the Old World. In this lesson, you might post an outline map of the continents on a bulletin board. Have students use library and/or Internet resources (provided below) to research some of the edible items the first explorers saw for the first time in the New World. On the bulletin board, draw an arrow from the New World (the Americas) to the Old World (Europe, Asia, Africa) and post around it drawings or images (from magazines or clip art) of products discovered in the New World and taken back to the Old World.
Soon, the explorers would introduce plants/foods from the Old World to the Americas. You might draw a second arrow on the board -- from the Old World to the New World -- and post appropriate drawings or images around it.
Adapt the Lesson for Younger Students
Younger students will not have the ability to research foods that originated in the New and Old World. You might adapt the lesson by sharing some of the food items in the Food Lists section below. Have students collect or draw pictures of those items for the bulletin board display.
Resources
In addition to library resources, students might use the following Internet sites as they research the geographic origins of some foods:
Curry, Spice, and All Things Nice: Food Origins
The Food Timeline
Native Foods of the Americas
A Harvest Gathered: Food in the New World
We Are What We Eat Timeline (Note: This resource is an archived resource; the original page is no longer live and updated.)
Food Lists Our research uncovered the Old and New World foods below. Students might find many of those and add them to the bulletin board display. Notice that some items appear on both lists -- beans, for example. There are many varieties of beans, some with New World origins and others with their origins in the Old World. In our research, we found sources that indicate onions originated in the New and sources that indicate onions originated in the Old World. Students might create a special question mark symbol to post next to any item for which contradictory sources can be found
Note: The Food Timeline is a resource that documents many Old World products. This resource sets up a number of contradictions. For example:
Many sources note that tomatoes originated in the New World; The Food Timeline indicates that tomatoes were introduced to the New World in 1781.
The Food Timeline indicates that strawberries and raspberries were available in the 1st century in Europe; other sources identify them as New World commodities.
Foods That Originated in the New World: artichokes, avocados, beans (kidney and lima), black walnuts, blueberries, cacao (cocoa/chocolate), cashews, cassava, chestnuts, corn (maize), crab apples, cranberries, gourds, hickory nuts, onions, papayas, peanuts, pecans, peppers (bell peppers, chili peppers), pineapples, plums, potatoes, pumpkins, raspberries, squash, strawberries, sunflowers, sweet potatoes, tobacco, tomatoes, turkey, vanilla, wild cherries, wild rice.
Foods That Originated in the Old World: apples, bananas, beans (some varieties), beets, broccoli, carrots, cattle (beef), cauliflower, celery, cheese, cherries, chickens, chickpeas, cinnamon, coffee, cows, cucumbers, eggplant, garlic, ginger, grapes, honey (honey bees), lemons, lettuce, limes, mangos, oats, okra, olives, onions, oranges, pasta, peaches, pears, peas, pigs, radishes, rice, sheep, spinach, tea, watermelon, wheat, yams.
Extension Activities
Home-school connection. Have students and their parents search their food cupboards at home; ask each student to bring in two food items whose origin can be traced to a specific place (foreign if possible, domestic if not). Labels from those products will be sufficient, especially if the products are in breakable containers. Place those labels/items around a world map; use yarn to connect each label to the location of its origin on the map.
Media literacy. Because students will research many sources, have them list the sources for the information they find about each food item. Have them place an asterisk or checkmark next to the food item each time they find that item in a different source. If students find a food in multiple sources, they might consider it "verified"; those foods they find in only one source might require additional research to verify.
Assessment
Invite students to agree or disagree with the following statement:The early explorers were surprised by many of the foods they saw in the New World.
Have students write a paragraph in support of their opinion.
Lesson Plan Source
Education World
Submitted By
Gary Hopkins
National Standards
LANGUAGE ARTS: EnglishGRADES K - 12NL-ENG.K-12.2 Reading for UnderstandingNL-ENG.K-12.8 Developing Research SkillsNL-ENG.K-12.9 Multicultural UnderstandingNL-ENG.K-12.12 Applying Language Skills
SOCIAL SCIENCES: EconomicsGRADES K - 4NSS-EC.K-4.1 Productive ResourcesNSS-EC.K-4.6 Gain from TradeGRADES 5 - 8NSS-EC.5-8.1 Productive ResourcesNSS-EC.5-8.6 Gain from TradeGRADES 9 - 12NSS-EC.9-12.1 Productive ResourcesNSS-EC.9-12.6 Gain from Trade
SOCIAL SCIENCES: GeographyGRADES K - 12NSS-G.K-12.1 The World in Spatial TermsNSS-G.K-12.2 Places and Regions
SOCIAL SCIENCES: U.S. HistoryGRADES K - 4NSS-USH.K-4.1 Living and Working together in Families and Communities, Now and Long AgoNSS-USH.K-4.3 The History of the United States: Democratic Principles and Values and the People from Many Cultures Who Contributed to Its Cultural, Economic, and Political HeritageNSS-USH.K-4.4 The History of Peoples of Many Cultures Around the WorldGRADES 5 - 12NSS-USH.5-12.1 Era 1: Three Worlds Meet (Beginnings to 1620)NSS-USH.5-12.2 Era 2: Colonization and Settlement (1585-1763)NSS-WH.5-12.6 Global Expansion and Encounter, 1450-1770
TECHNOLOGYGRADES K - 12NT.K-12.1 Basic Operations and ConceptsNT.K-12.5 Technology Research Tools
Find many more great geography lesson ideas and resources in Education World's Geography Center.
Click here to return to this week's World of Learning lesson plan page.
Updated 10/11/12
Back to Geography Lesson Plan
Where Did Foods Originate?
(Foods of the New World and Old World)
Subjects
Arts & Humanities
--Language Arts
Educational Technology
Science
--Agriculture
Social Studies
--Economics
--Geography
--History
----U.S. History
----World History
--Regions/Cultures
Grade
K-2
3-5
6-8
9-12
Advanced
Brief Description
Students explore how New World explorers helped change the Old World's diet (and vice versa).
Objectives
Students will
learn about changes that occurred in the New World and Old World as a result of early exploration.
use library and Internet sources to research food origins. (Older students only.)
create a bulletin-board map illustrating the many foods that were shared as a result of exploration.
Keywords
Columbus, explorers, origin, food, timeline, plants, map, New World, Old World, colonies, colonial, crops, media literacy, products, consumer
Materials Needed:
library and/or Internet access (older students only)
outline map of the world (You might print the map on a transparency; then use an overhead projector to project and trace a large outline map of the world onto white paper on a bulletin board.)
magazines (optional)
Lesson Plan
The early explorers to the Americas were exposed to many things they had never seen before. Besides strange people and animals, they were exposed to many foods that were unknown in the Old World. In this lesson, you might post an outline map of the continents on a bulletin board. Have students use library and/or Internet resources (provided below) to research some of the edible items the first explorers saw for the first time in the New World. On the bulletin board, draw an arrow from the New World (the Americas) to the Old World (Europe, Asia, Africa) and post around it drawings or images (from magazines or clip art) of products discovered in the New World and taken back to the Old World.
Soon, the explorers would introduce plants/foods from the Old World to the Americas. You might draw a second arrow on the board -- from the Old World to the New World -- and post appropriate drawings or images around it.
Adapt the Lesson for Younger Students
Younger students will not have the ability to research foods that originated in the New and Old World. You might adapt the lesson by sharing some of the food items in the Food Lists section below. Have students collect or draw pictures of those items for the bulletin board display.
Resources
In addition to library resources, students might use the following Internet sites as they research the geographic origins of some foods:
Curry, Spice, and All Things Nice: Food Origins
The Food Timeline
Native Foods of the Americas
A Harvest Gathered: Food in the New World
We Are What We Eat Timeline (Note: This resource is an archived resource; the original page is no longer live and updated.)
Food Lists Our research uncovered the Old and New World foods below. Students might find many of those and add them to the bulletin board display. Notice that some items appear on both lists -- beans, for example. There are many varieties of beans, some with New World origins and others with their origins in the Old World. In our research, we found sources that indicate onions originated in the New and sources that indicate onions originated in the Old World. Students might create a special question mark symbol to post next to any item for which contradictory sources can be found
Note: The Food Timeline is a resource that documents many Old World products. This resource sets up a number of contradictions. For example:
Many sources note that tomatoes originated in the New World; The Food Timeline indicates that tomatoes were introduced to the New World in 1781.
The Food Timeline indicates that strawberries and raspberries were available in the 1st century in Europe; other sources identify them as New World commodities.
Foods That Originated in the New World: artichokes, avocados, beans (kidney and lima), black walnuts, blueberries, cacao (cocoa/chocolate), cashews, cassava, chestnuts, corn (maize), crab apples, cranberries, gourds, hickory nuts, onions, papayas, peanuts, pecans, peppers (bell peppers, chili peppers), pineapples, plums, potatoes, pumpkins, raspberries, squash, strawberries, sunflowers, sweet potatoes, tobacco, tomatoes, turkey, vanilla, wild cherries, wild rice.
Foods That Originated in the Old World: apples, bananas, beans (some varieties), beets, broccoli, carrots, cattle (beef), cauliflower, celery, cheese, cherries, chickens, chickpeas, cinnamon, coffee, cows, cucumbers, eggplant, garlic, ginger, grapes, honey (honey bees), lemons, lettuce, limes, mangos, oats, okra, olives, onions, oranges, pasta, peaches, pears, peas, pigs, radishes, rice, sheep, spinach, tea, watermelon, wheat, yams.
Extension Activities
Home-school connection. Have students and their parents search their food cupboards at home; ask each student to bring in two food items whose origin can be traced to a specific place (foreign if possible, domestic if not). Labels from those products will be sufficient, especially if the products are in breakable containers. Place those labels/items around a world map; use yarn to connect each label to the location of its origin on the map.
Media literacy. Because students will research many sources, have them list the sources for the information they find about each food item. Have them place an asterisk or checkmark next to the food item each time they find that item in a different source. If students find a food in multiple sources, they might consider it "verified"; those foods they find in only one source might require additional research to verify.
Assessment
Invite students to agree or disagree with the following statement:The early explorers were surprised by many of the foods they saw in the New World.
Have students write a paragraph in support of their opinion.
Lesson Plan Source
Education World
Submitted By
Gary Hopkins
National Standards
LANGUAGE ARTS: EnglishGRADES K - 12NL-ENG.K-12.2 Reading for UnderstandingNL-ENG.K-12.8 Developing Research SkillsNL-ENG.K-12.9 Multicultural UnderstandingNL-ENG.K-12.12 Applying Language Skills
SOCIAL SCIENCES: EconomicsGRADES K - 4NSS-EC.K-4.1 Productive ResourcesNSS-EC.K-4.6 Gain from TradeGRADES 5 - 8NSS-EC.5-8.1 Productive ResourcesNSS-EC.5-8.6 Gain from TradeGRADES 9 - 12NSS-EC.9-12.1 Productive ResourcesNSS-EC.9-12.6 Gain from Trade
SOCIAL SCIENCES: GeographyGRADES K - 12NSS-G.K-12.1 The World in Spatial TermsNSS-G.K-12.2 Places and Regions
SOCIAL SCIENCES: U.S. HistoryGRADES K - 4NSS-USH.K-4.1 Living and Working together in Families and Communities, Now and Long AgoNSS-USH.K-4.3 The History of the United States: Democratic Principles and Values and the People from Many Cultures Who Contributed to Its Cultural, Economic, and Political HeritageNSS-USH.K-4.4 The History of Peoples of Many Cultures Around the WorldGRADES 5 - 12NSS-USH.5-12.1 Era 1: Three Worlds Meet (Beginnings to 1620)NSS-USH.5-12.2 Era 2: Colonization and Settlement (1585-1763)NSS-WH.5-12.6 Global Expansion and Encounter, 1450-1770
TECHNOLOGYGRADES K - 12NT.K-12.1 Basic Operations and ConceptsNT.K-12.5 Technology Research Tools
Find many more great geography lesson ideas and resources in Education World's Geography Center.
Click here to return to this week's World of Learning lesson plan page.
Updated 10/11/12 Having a tough time finding the right words to come up with "areas for improvement" comments on your students' report cards? Check out our helpful suggestions to find just the right one!
The following statements will help you tailor your comments to specific children and highlight their areas for improvement.
Be sure to check out our 125 Report Card Comments for positive comments!
Needs Improvement- all topics
is a hard worker, but has difficulty staying on task.
has a difficult time staying on task and completing his/her work.
needs to be more respectful and courteous to his/her classmates.
needs to listen to directions fully so that he/she can learn to work more independently.
is not demonstrating responsibility and needs to be consistently reminded of how to perform daily classroom tasks.
works well alone, but needs to learn how to work better cooperatively with peers.
does not have a positive attitude about school and the work that needs to be completed.
struggles with completing his/her work in a timely manner.
gives up easily when something is difficult and needs extensive encouragement to attempt the task.
gets along with his/her classmates well, but is very disruptive during full group instruction.
has a difficult time using the materials in the classroom in a respectful and appropriate manner.
has a difficult time concentrating and gets distracted easily.
is having a difficult time with math. Going over _____ at home would help considerably.
is having a very difficult time understanding math concepts for his/her grade level. He/she would benefit from extra assistance.
could benefit from spending time reading with an adult every day.
is enthusiastic, but is not understanding ____. Additional work on these topics would be incredibly helpful.
is having difficulty concentrating during math lessons and is not learning the material that is being taught because of that.
understands math concepts when using manipulatives, but is having a difficult time learning to ____ without them.
is a very enthusiastic reader. He/she needs to continue to work on _____ to make him/her a better reader.
needs to practice reading at home every day to help make him/her a stronger reader.
needs to practice his/her sight words so that he/she knows them on sight and can spell them.
needs to work on his/her spelling. Practicing at home would be very beneficial.
can read words fluently, but has a difficult time with comprehension. Reading with ______ every day would be helpful.
could benefit from working on his/her handwriting. Slowing down and taking more time would help with this.
is having difficulty writing stories. Encouraging him/her to tell stories at home would help with this.
has a difficult time knowing when it is appropriate to share his/her thoughts. We are working on learning when it is a good time to share and when it is a good time to listen.
needs to work on his/her time management skills. _______is able to complete his/her work, but spends too much time on other tasks and rarely completes his/her work.
needs reminders about the daily classroom routine. Talking through the classroom routine at home would be helpful.
is having a difficult time remembering the difference between short and long vowel sounds. Practicing these at home would be very helpful.
is struggling with reading. He/she does not seem to enjoy it and does not want to do it. Choosing books that he/she like and reading them with him/her at home will help build a love of reading.
frequently turns in incomplete homework or does not hand in any homework. Encouraging _______to complete his/her homework would be very helpful.
does not take pride in his/her work. We are working to help him/her feel good about what he/she accomplishes.
does not actively participate in small group activities. Active participation would be beneficial.
has a difficult time remembering to go back and check his/her work. Because of this, there are often spelling and grammar mistakes in his/her work.
does not much effort into his/her writing. As a result, his/her work is often messy and incomplete.
is struggling to understand new concepts in science. Paying closer attention to the class discussions and the readings that we are doing would be beneficial.
is reading significantly below grade level. Intervention is required.
does not write a clear beginning, middle and end when writing a story. We are working to identify the parts of the stories that he/she is writing.
is struggling to use new reading strategies to help him/her read higher level books.
is wonderful at writing creative stories, but needs to work on writing nonfiction and using facts.
has a difficult time understanding how to solve word problems.
needs to slow down and go back and check his/her work to make sure that all answers are correct.
is not completing math work that is on grade level. Intervention is required.
is struggling to understand place value.
is very enthusiastic about math, but struggles to understand basic concepts.
has a difficult time remembering the value of different coins and how to count them. Practicing this at home would be helpful.
would benefit from practicing math facts at home.
is very engaged during whole group math instruction, but struggles to work independently.
is able to correctly answer word problems, but is unable to explain how he/she got the answer.
is having a difficult time comparing numbers.
Related: 125 Report Card Comments for positive comments!
Student Award Certificates!
Recognize positive attitudes and achievements with personalized student award certificates!
Copyright© 2020 Education World
Having a tough time finding the right words to come up with "areas for improvement" comments on your students' report cards? Check out our helpful suggestions to find just the right one!
The following statements will help you tailor your comments to specific children and highlight their areas for improvement.
Be sure to check out our 125 Report Card Comments for positive comments!
Needs Improvement- all topics
is a hard worker, but has difficulty staying on task.
has a difficult time staying on task and completing his/her work.
needs to be more respectful and courteous to his/her classmates.
needs to listen to directions fully so that he/she can learn to work more independently.
is not demonstrating responsibility and needs to be consistently reminded of how to perform daily classroom tasks.
works well alone, but needs to learn how to work better cooperatively with peers.
does not have a positive attitude about school and the work that needs to be completed.
struggles with completing his/her work in a timely manner.
gives up easily when something is difficult and needs extensive encouragement to attempt the task.
gets along with his/her classmates well, but is very disruptive during full group instruction.
has a difficult time using the materials in the classroom in a respectful and appropriate manner.
has a difficult time concentrating and gets distracted easily.
is having a difficult time with math. Going over _____ at home would help considerably.
is having a very difficult time understanding math concepts for his/her grade level. He/she would benefit from extra assistance.
could benefit from spending time reading with an adult every day.
is enthusiastic, but is not understanding ____. Additional work on these topics would be incredibly helpful.
is having difficulty concentrating during math lessons and is not learning the material that is being taught because of that.
understands math concepts when using manipulatives, but is having a difficult time learning to ____ without them.
is a very enthusiastic reader. He/she needs to continue to work on _____ to make him/her a better reader.
needs to practice reading at home every day to help make him/her a stronger reader.
needs to practice his/her sight words so that he/she knows them on sight and can spell them.
needs to work on his/her spelling. Practicing at home would be very beneficial.
can read words fluently, but has a difficult time with comprehension. Reading with ______ every day would be helpful.
could benefit from working on his/her handwriting. Slowing down and taking more time would help with this.
is having difficulty writing stories. Encouraging him/her to tell stories at home would help with this.
has a difficult time knowing when it is appropriate to share his/her thoughts. We are working on learning when it is a good time to share and when it is a good time to listen.
needs to work on his/her time management skills. _______is able to complete his/her work, but spends too much time on other tasks and rarely completes his/her work.
needs reminders about the daily classroom routine. Talking through the classroom routine at home would be helpful.
is having a difficult time remembering the difference between short and long vowel sounds. Practicing these at home would be very helpful.
is struggling with reading. He/she does not seem to enjoy it and does not want to do it. Choosing books that he/she like and reading them with him/her at home will help build a love of reading.
frequently turns in incomplete homework or does not hand in any homework. Encouraging _______to complete his/her homework would be very helpful.
does not take pride in his/her work. We are working to help him/her feel good about what he/she accomplishes.
does not actively participate in small group activities. Active participation would be beneficial.
has a difficult time remembering to go back and check his/her work. Because of this, there are often spelling and grammar mistakes in his/her work.
does not much effort into his/her writing. As a result, his/her work is often messy and incomplete.
is struggling to understand new concepts in science. Paying closer attention to the class discussions and the readings that we are doing would be beneficial.
is reading significantly below grade level. Intervention is required.
does not write a clear beginning, middle and end when writing a story. We are working to identify the parts of the stories that he/she is writing.
is struggling to use new reading strategies to help him/her read higher level books.
is wonderful at writing creative stories, but needs to work on writing nonfiction and using facts.
has a difficult time understanding how to solve word problems.
needs to slow down and go back and check his/her work to make sure that all answers are correct.
is not completing math work that is on grade level. Intervention is required.
is struggling to understand place value.
is very enthusiastic about math, but struggles to understand basic concepts.
has a difficult time remembering the value of different coins and how to count them. Practicing this at home would be helpful.
would benefit from practicing math facts at home.
is very engaged during whole group math instruction, but struggles to work independently.
is able to correctly answer word problems, but is unable to explain how he/she got the answer.
is having a difficult time comparing numbers.
Related: 125 Report Card Comments for positive comments!
Student Award Certificates!
Recognize positive attitudes and achievements with personalized student award certificates!
Copyright© 2020 Education World




